צווישן די פאַרשידן פאָרקאַסטינג מעטהאָדס, איינער קען נישט נאָר ויסשליסן די אַפּראַקסאַמיישאַן. ניצן עס, איר קענען מאַכן פּראָסט עסטאַמאַץ און רעכענען די פּלאַננעד ינדאַקייטערז דורך ריפּלייסינג די אָריגינעל אַבדזשעקץ מיט סימפּלער אָנעס. אין עקססעל, עס איז אויך די מעגלעכקייט צו נוצן דעם אופֿן פֿאַר פאָרויסזאָגן און אַנאַליסיס. זאל ס קוק אין ווי דעם אופֿן קענען זיין געווענדט אין די ספּעסיפיעד פּראָגראַם מיט אַ געבויט-אין מכשירים.
אַפּפּראָקסימאַטיאָן
דער נאָמען פון דעם אופֿן קומט פון די לאַטייַן וואָרט פּראַקסימאַ - "קלאָוסאַסט". עס איז אַפּראַקסאַמיישאַן דורך סימפּלאַפיקיישאַן און סמודינג פון באַוווסט ינדאַקייטערז, און בויען זיי אין אַ גאַנג וואָס איז די יקער. אָבער דעם אופֿן קענען זיין געניצט ניט בלויז פֿאַר פאָרויסזאָגן, אָבער אויך צו לערנען יגזיסטינג רעזולטאַטן. דערנאָך, אַפּפּראָקסימאַטיאָן איז, אין פאַקט, אַ סימפּלאַפיקיישאַן פון די מקור דאַטן, און אַ סימפּלאַפייד ווערסיע איז גרינגער צו ויספאָרשן.
די הויפּט געצייַג מיט וואָס סמודינג איז דורכגעקאָכט אין עקססעל איז די קאַנסטראַקשאַן פון אַ גאַנג שורה. די דנאָ שורה איז אַז, באזירט אויף יגזיסטינג ינדאַקייטערז, אַ פונקציע גראַפיק פֿאַר צוקונפֿט פּיריאַדז איז געענדיקט. דער הויפּט ציל פון דעם גאַנג שורה איז, ווי איר קען טרעפן, צו מאַכן פאָרקאַסץ אָדער ידענטיפיצירן אַ גענעראַל גאַנג.
אָבער עס קענען זיין קאַנסטראַקטאַד מיט איינער פון פינף טייפּס פון אַפּפּראָקסימאַטיאָן:
- לינעאַר;
- עקספּאָונענשאַל;
- Logarithmic;
- פּאָלינאָומיאַל;
- מאַכט.
מיר באַטראַכטן יעדער פון די אָפּציעס אין מער דעטאַל סעפּעראַטלי.
לעקציע: ווי צו בויען אַ גאַנג שורה אין עקססעל
אופֿן 1: לינעאַר סמודינג
לאָמיר קודם קוק די סימפּלאַסט אַפּראַקסאַמיישאַן אָפּציע, ניימלי ניצן אַ לינעאַר פונקציע. מיר וועלן דאַוונען עס אין מער דעטאַל, ווייַל מיר וועלן ויסשיקן די אַלגעמיינע פונקטן וואָס זענען כאַראַקטעריסטיש פֿאַר אנדערע מעטהאָדס, ניימלי די קאַנסטראַקשאַן פון אַ פּלאַן און עטלעכע אנדערע נואַנסיז וואָס מיר וועלן נישט וווינען אויף ווען איר באַטראַכטן די פאלגענדע אָפּציעס.
ערשטער פון אַלע, מיר בויען אַ גראַפיק אויף די יקער פון וואָס מיר דורכפירן די סמודינג פּראָצעדור. צו בויען אַ פּלאַן, מיר נעמען אַ טיש אין וואָס די כוידעשלעך פּרייַז פון אַ פּראָדוקציע אַפּאַראַט געשאפן דורך די פאַרנעמונג און די קאָראַספּאַנדינג נוץ אין אַ געוויסע צייט זענען אנגעוויזן. די גראַפיק פונקציע וואָס מיר בויען וועט פאַרטראַכטן די אָפענגיקייַט פון די פאַרגרעסערן אין נוץ אויף די פאַרקלענערן אין די פּראָדוקציע פּראָדוקציע קאָס.
- צו פּלאַנעווען, ערשטער פון אַלע, סעלעקטירן די שפאלטן "יוניט קאסט" און נוץ. נאָך דעם, מאַך צו די קוויטל אַרייַנלייגן. דריקט אויף די בענד אין די טשאַרץ מכשירים קעסטל "ספּאָט". סעלעקטירן דעם נאָמען אין דער רשימה וואָס אָפּענס "ספּאָט מיט גלאַט קורוועס און מאַרקערס". עס איז דעם טיפּ פון טשאַרט וואָס איז מערסט פּאַסיק פֿאַר ארבעטן מיט אַ גאַנג שורה, און דעריבער אַפּלייז די אַפּראַקסאַמיישאַן אופֿן אין עקססעל.
- דער פּלאַן איז געבויט.
- צו לייגן אַ גאַנג שורה, סעלעקטירן עס דורך קליקינג די רעכט מויז קנעפּל. א קאָנטעקסט מעניו איז ארויס. קלייַבן די נומער אין עס "לייג אַ גאַנג שורה ...".
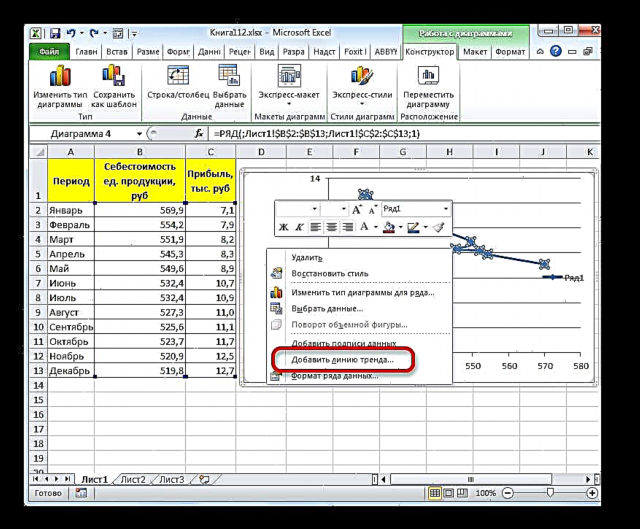
עס איז אן אנדער אָפּציע צו לייגן עס. אין אַ נאָך גרופּע פון טאַבס אויף די בענד "ארבעטן מיט טשאַרץ" מאַך צו די קוויטל "אויסלייג". ווייַטער אין די מכשירים בלאָק "אַנאַליסיס" דריקט אויף די קנעפּל גאַנג ליניע. די רשימה אָפּענס. זינט מיר דאַרפֿן צו צולייגן אַ לינעאַר אַפּראַקסאַמיישאַן, מיר סעלעקטירן פֿון די דערלאנגט שטעלעס "לינעאַר אַפּראַקסאַמיישאַן".
- אויב איר פונדעסטוועגן אויסדערוויילט דער ערשטער אָפּציע מיט אַדינג אַקשאַנז דורך די קאָנטעקסט מעניו, אַ פֿאָרמאַט פֿענצטער וועט זיין אָופּאַנד.
אין די בלאָק פון פּאַראַמעטערס "בילדינג אַ גאַנג שורה (אַפּראַקסאַמיישאַן און סמודינג)" שטעלן די באַשטימען צו די שטעלע "לינעאַר".
אויב איר ווילט, איר קענט קעסטל די קעסטל ווייַטער צו די שטעלע "ווייַזן יקווייזשאַן אין דיאַגראַמע". דערנאָך, די יקווייזשאַן פון די סמודינג פונקציע וועט זיין געוויזן אויף די דיאַגראַמע.אין אונדזער פאַל, צו פאַרגלייכן פאַרשידענע אַפּפּראָקסימאַטיאָן אָפּציעס, עס איז וויכטיק צו קאָנטראָלירן די קעסטל לעבן "שטעלן אויף די טשאַרט די ווערט פון פאַרלאָזלעך אַפּראַקסאַמיישאַן (R ^ 2)". דעם גראדן קען זיין אַנדערש פון 0 פריער 1. די העכער עס איז, די אַפּפּראָקסימאַטיאָן איז בעסער (מער פאַרלאָזלעך). עס איז געמיינט אַז מיט דעם ווערט פון דעם גראדן 0,85 די סמאָאָטהיע קענען זיין גערעכנט ווי פאַרלאָזלעך, אָבער אויב די גראדן איז נידעריקער, ניט.
נאָך אַלע די סעטטינגס אויבן. דריקט אויף די קנעפּל נאָענטליגן אין די דנאָ פון די פֿענצטער.
- ווי איר קענען זען, די גאַנג שורה איז פּלאָטעד אויף די טשאַרט. מיט אַ לינעאַר אַפּראַקסאַמיישאַן, עס איז אנגעוויזן דורך אַ שוואַרץ גלייַך שורה. די ספּעציפיצירט טיפּ פון סמודינג קענען זיין געוויינט אין די סימפּלאַסט קאַסעס ווען די דאַטן ענדערונגען גאַנץ געשווינד און די אָפענגיקייט פון די פונקציע ווערט פון די אַרגומענט איז קלאָר ווי דער טאָג.





די סמודינג וואָס איז געניצט אין דעם פאַל איז דיסקרייבד דורך די פאלגענדע פאָרמולע:
y = אַקס + ב
אין אונדזער באַזונדער פאַל, די פאָרמולע נעמט די פאלגענדע פאָרעם:
y = -0.1156x + 72.255
די אַפּוינטמאַנט פון די אַקיעראַסי ווערט גלייך 0,9418וואָס איז אַ גאַנץ פּאַסיק רעזולטאַט וואָס קעראַקטערייז סמודינג ווי פאַרלאָזלעך.
אופֿן 2: עקספּאָונענשאַל אַפּפּראָקסימאַטיאָן
איצט לאָזן אַ קוק אין די עקספּאָונענשאַל אַפּפּראָקסימאַטיאָן אין עקססעל.
- צו טוישן דעם טיפּ פון דער גאַנג שורה, סעלעקטירן עס דורך קליקינג די רעכט מויז קנעפּל און סעלעקטירן דעם נומער אין דעם קנאַל-אַרויף מעניו. "די פֿאָרמאַט פון דער גאַנג ליניע ...".
- דערנאָך, די באַקאַנט פֿאָרמאַט פֿענצטער. שטעלן די באַשטימען צו די סעלעקציע פאַרשפּאַרן טיפּ "עקספּאָונענשאַל". די רוען סעטטינגס וועט בלייַבן די זעלבע ווי אין דער ערשטער פאַל. דריקט אויף די קנעפּל נאָענט.
- נאָך דעם, די גאַנג שורה וועט זיין פּלאַטעד אויף די טשאַרט. ווי איר קענען זען, עס איז אַ ביסל קערווד פאָרעם ווען איר נוצן דעם אופֿן. אין דעם פאַל, די צוטרוי איז 0,9592וואָס איז העכער ווי ווען ניצן לינעאַר אַפּראַקסאַמיישאַן. די עקספּאָונענשאַל אופֿן איז בעסטער געניצט ווען די וואַלועס געשווינד טוישן און דאַן נעמען אַ באַלאַנסט פאָרעם.



די אַלגעמיינע פאָרעם פון די סמודינג פונקציע איז ווי גייט:
y = זיין ^ x
ווו e איז די יקער פון די נאַטירלעך לאָגאַריטהם.
אין אונדזער באַזונדער פאַל, די פאָרמולע האט די פאלגענדע פאָרעם:
y = 6282.7 * e ^ (- 0.012 * x)
אופֿן 3: לאָגאַריטהמיק סמודינג
איצט עס איז דער קער צו באַטראַכטן דעם אופֿן פון לאָגאַריטהמיק אַפּראַקסאַמיישאַן.
- אין דער זעלביקער וועג ווי די פריערדיקע מאָל, מיר קאַטער די פֿענצטער פֿאָרמאַט טרענד ליניע דורך די קאָנטעקסט מעניו. שטעלן די באַשטימען צו די שטעלע "Logarithmic" און גיט די קנעפּל נאָענט.
- עס איז אַ פּראָצעדור פֿאַר קאַנסטראַקטינג אַ גאַנג ליניע מיט אַ לאַגערידמיק אַפּראַקסאַמיישאַן. ווי אין דעם פריערדיקן פאַל, די אָפּציע איז בעסטער געניצט ווען די דאַטן טכילעס ענדערונגען געשווינד און דאַן אַ באַלאַנסט קוק. ווי איר קענט, די צוטרוי ראַנג איז 0.946. דאָס איז העכער ווי ניצן די לינעאַר אופֿן, אָבער נידעריקער ווי די קוואַליטעט פון דער גאַנג שורה מיט עקספּאָונענשאַל סמודינג.


אין אַלגעמיין, די סמודינג פאָרמולע קוקט אַזוי:
y = a * ln (x) + b
ווו ln איז די ווערט פון די נאַטירלעך לאָגאַריטהם. דערפאר די נאָמען פון דעם אופֿן.
אין אונדזער פאַל, די פאָרמולע נעמט די פאלגענדע פאָרעם:
y = -62.81ln (x) +404.96
אופֿן 4: פּאָלינום סמודינג
די צייט איז געקומען צו באַטראַכטן די מעטהאָדס פון פּאָלינום סמודינג.
- גיין צו די פֿענצטער גאַנג פון די גאַנג שורה, ווי שוין געטאן מער ווי איין מאָל. אין בלאָק "בילדינג אַ גאַנג ליניע" שטעלן די באַשטימען צו די שטעלע "פּאָלינאָומיאַל". צו די רעכט פון דעם נומער איז אַ פעלד "גראַד". ווען טשוזינג אַ ווערט "פּאָלינאָומיאַל" עס ווערט אקטיוו. דאָ איר קענען ספּעציפיצירן קיין מאַכט ווערט פֿון 2 (באַשטעטיקט דורך פעליקייַט) צו 6. דעם גראדן דיטערמאַנז די נומער פון מאַקסימאַ און מינימאַ פון די פונקציע. ווען ינסטאָלינג אַ פּאָלינאָמיאַל פון די רגע גראַד, בלויז איין מאַקסימום איז דיסקרייבד, און ווען ינסטאָלינג אַ פּאָלינאָמיאַל פון די זעקסט גראַד קענען זיין דיסקרייבד אַרויף צו פינף מאַקסימאַ. קודם לאָזן די פעליקייַט סעטטינגס, דאָס איז, מיר וועלן אָנווייַזן די רגע גראַד. די איבעריקע סעטטינגס לאָזן די זעלבע ווי אין די פריערדיקע מעטהאָדס. דריקט אויף די קנעפּל נאָענט.
- די גאַנג שורה ניצן דעם אופֿן איז פּלאַטעד. ווי איר קענען זען, עס איז אפילו מער קערווד ווי ווען איר נוצן עקספּאָונענשאַל אַפּראַקסאַמיישאַן. די צוטרוי שטאַפּל איז העכער ווי מיט קיין פון די פריער געוויינט מעטהאָדס, און איז 0,9724.

דער מעטאָד איז מערסט הצלחה אַפּלייז אויב די דאַטן זענען קעסיידערדיק. די פונקציע וואָס באשרייבט דעם סמודינג טיפּ קוקט אַזוי:
y = a1 + a1 * x + a2 * x ^ 2 + ... + an * x ^ nאין אונדזער פאַל, די פאָרמולע האט די פאלגענדע פאָרעם:
y = 0.0015 * x ^ 2-1.7202 * x + 507.01 - לאָמיר איצט טוישן די גראַד פון פּאָלינאַמיאַלז צו זען אויב דער רעזולטאַט וועט זיין אַנדערש. מיר צוריקקומען צו די פֿאָרמאַט פֿענצטער. מיר לאָזן די אַפּראָוטאַמיישאַן טיפּ פּאָלינאָמיאַל, אָבער אַנטקעגן דעם, אין די גראַד פֿענצטער, שטעלן די מאַקסימום מעגלעך ווערט - 6.
- ווי איר קענט, נאָך דעם, אונדזער גאַנג שורה גענומען די פאָרעם פון אַ פּראַנאַונסט ויסבייג, אין וואָס די נומער פון מאַקסימאַ איז זעקס. די צוטרוי שטאַפּל געוואקסן אפילו מער, אַמאַוניד צו 0,9844.



די פאָרמולע וואָס באשרייבט דעם טיפּ פון סמודינג נעמט די פאלגענדע פאָרעם:
y = 8E-08x ^ 6-0,0003x ^ 5 + 0,3725x ^ 4-269,33x ^ 3 + 109525x ^ 2-2E + 07x + 2E + 09
אופֿן 5: מאַכט סמודינג
אין מסקנא, מיר באַטראַכטן די מאַכט-געזעץ אַפּראַקסאַמיישאַן אופֿן אין עקססעל.
- מיר מאַך צו די פֿענצטער גאַנג ליניע פֿאָרמאַטירונג. שטעלן דעם טיפּ פון סמודינג באַשטימען צו שטעלע "מאַכט". די אַרויסווייַזן פון די יקווייזשאַן און די צוטרוי מדרגה, ווי שטענדיק, איז לינקס אויף. דריקט אויף די קנעפּל נאָענט.
- דער פּראָגראַם פארמען אַ גאַנג שורה. ווי איר קענען זען, אין אונדזער פאַל, עס איז אַ שורה מיט אַ קליין בייגן. די צוטרוי שטאַפּל איז 0,9618וואָס איז אַ שיין הויך קורס. פון אַלע די אויבן מעטהאָדס, די צוטרוי מדרגה איז געווען העכער בלויז ווען ניצן די פּאָלינאָומיאַל אופֿן.


דעם אופֿן איז יפעקטיוולי געניצט אין קאַסעס פון אינטענסיווע ענדערונג פון פונקציאָנירן דאַטן. עס איז וויכטיק צו באַטראַכטן אַז די אָפּציע איז אָנווענדלעך בלויז אונטער די צושטאַנד אַז די פונקציע און אַרגומענט טאָן ניט אָננעמען נעגאַטיוו וואַלועס אָדער נול.
דער גענעראַל פאָרמולע וואָס דיסקרייבז דעם אופֿן האט די פאלגענדע פאָרעם:
y = bx ^ n
אין אונדזער באַזונדער פאַל, עס קוקט ווי דאָס:
y = 6E + 18x ^ (- 6.512)
ווי איר קענט זען די ספּעציפיש דאַטן וואָס מיר געוויינט ווי אַ ביישפּיל, די מעטהאָדס פון אַפּפּראָקסימאַטיאָן פון פּאָלינאָמיאַל צו די זעקסט גראַד געוויזן די העכסטן שטאַפּל פון רילייאַבילאַטי (0,9844), די לאָואַסט מדרגה פון בטחון אין די לינעאַר אופֿן (0,9418) אָבער דאָס קען נישט מיינען אַז די זעלבע טענדענץ וועט זיין ביי אנדערע ביישפילן. ניין, די עפעקטיווקייט הייך פון די מעטהאָדס אויבן קענען בייַטן באטייטיק, דיפּענדינג אויף די ספּעציפיש טיפּ פון פונקציע פֿאַר וואָס די גאַנג שורה וועט זיין געבויט. דעריבער, אויב די סעלעקטעד מעטאָד איז מערסט עפעקטיוו פֿאַר דעם פונקציע, דאָס טוט נישט מיינען אין אַלע אַז עס וועט אויך זיין אָפּטימאַל אין אן אנדער סיטואַציע.
אויב איר קען נישט באַשליסן גלייך, באזירט אויף די רעקאַמאַנדיישאַנז אויבן, וואָס טיפּ פון אַפּפּראָקסימאַטיאָן איז פּאַסיק ספּאַסיפיקלי פֿאַר דיין פאַל, דעמאָלט עס איז זינען צו פּרובירן אַלע מעטהאָדס. נאָך בויען אַ גאַנג שורה און וויוינג זיין בטחון מדרגה, עס איז מעגלעך צו קלייַבן די בעסטער אָפּציע.